如何利用Kelly公式，优化FOF组合的配置权重？

2. Kelly公式在基金组合配置中的应用

之前我们对基金组合进行了一些列绝对收益型策略的开发，包括股债配置策略、债券配置策略、类固收资产配置策略，从自上而下的逻辑看，基金组合配置取决于三个因素：一是宏观大类资产配置权重，二是中观策略或风格配置权重，三是同一风格或策略内部的微观资产间的权重分配，其中前两者研究在于对资产和风格的研判，而对于具体同一类型的基金权重如何分配，通常的做法是采用等权重加权，一方面是因为简单清晰，同时也表明对于基金收益未来无法估计的情况下，等权重加权是一种获得平均收益的方式，当然也有采用基于风险平价的方式，目的是不希望在某一标的风险暴露过高，但他们往往可能损失了优质基金的超额收益。Kelly公式的目标是选择最优投资比例使得资产的长期几何收益最大化，更加注重收益的可能性，因此我们尝试将Kelly公式应用至基金产品权重配置问题上。

为了检验不同方法加权效果，我们以公募基金中的债券型基金、混合型基金以及股票型基金作为测试的样本，他们的特点是权益仓位比例逐渐提高，收益的波动也随之提升。

对于每一类样本，为了控制组合所持基金数量多少对不同配置方法的影响，我们分别将组合所持有的基金数量设定为5只、10只以及20只（用N表示），并依次进行测试。我们以每个季末结束后的第一个月末（即每年1月、4月、7月、10月底）为换仓日，在换仓日随机选取N只基金，并采用不同的加权方式生成权重，最终生成组合净值。由于单次筛选产生的结果可能具有偶然性，为尽量客观比较不同权重配置方法的优劣，我们重复上述测试20次，并取平均值作为最终测试结果。为了比较不同测试方法的效果，我们主要从收益、风险以及收益风险比三个维度进行分析。测试时间从2015年1月至2020年10月30日。

模型参数设定：

（1）Kelly公式：对于伯努利分布下的Kelly公式，涉及到两个参数，胜率p和盈亏比a，由于考虑季度频率的配置，因此需估计季度频率的胜率和盈亏比，我们采用过去5年为统计区间，滚动60个交易日为周期，计算收益大于0的占比值作为胜率，盈利的平均值除以亏损的平均值作为基金季度的盈亏比。对于正态分布下的Kelly公式，涉及到资产的收益和波动率的估计，同样我们采用过去5年计算基金的年化收益和年化波动率作为代表。

（2）风险平价模型：采用过去5年的年化波动率作为基金波动率的代表。我们将风险平价模型的配置结果作为Kelly公式配置结果的比较依据。

此外，我们计算了等权配置的结果，一并进行比较。

2.1. 债券型基金组合测试结果

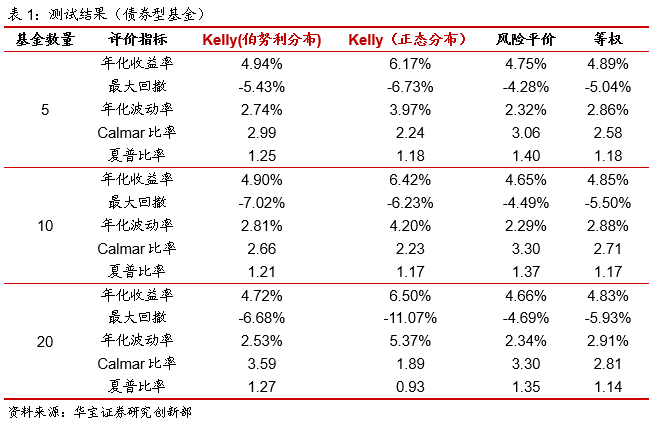
对于债券型基金，该类基金的收益和风险均较低，以等权重的结果作为代表，年化收益在5%左右，年化波动率在3%左右，最大回撤-5%，夏普比率在1.2左右。对于不同的加权方法，我们发现对于不同的基金数量下，采用Kelly公式加权的收益整体高于其他方法，尤其是正态分布下的Kelly公式，年化收益大于6%，但是最大回撤和波动率也相应扩大，最大回撤高于6%，甚至最高达到11%，年化波动率在4%左右，远远高于平均水平，另一方面风险平价收益略低于等权，但是回撤和年化波动率是最低的，最大回撤在5%以下，年化波动率在2.3%左右。总体从收益风险比的角度，风险平价模型是最高，Calmar比率高于3，夏普比率整体高于1.3。

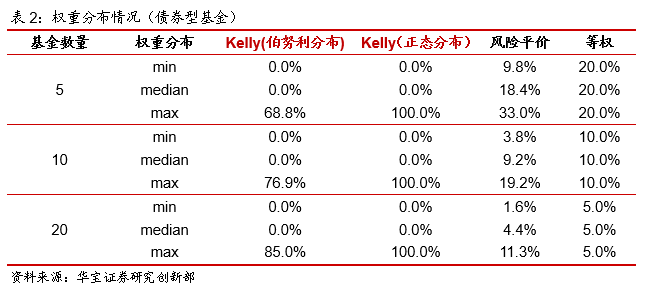
我们统计了不同加权方法的权重分布情况，根据每期权重的最大值、最小值以及中位数进行统计，汇总结果采用数据的中位数，从统计结果可以看出，Kelly公式权重偏离较大，尤其是正态分布下的Kelly的配置结果，几乎全部配置到某只基金，而风险平价在等权重附近偏离一定的幅度。

我们在测试其他类型的基金也同样发现了同样的问题，这是因为求解Kelly公式最优化问题时，其资产权重处于0~1的约束条件导致求解结果位于边界上，使得一部分基金配置权重过于集中，一部分没有进行配置。而我们实际配置中是在选出几只基金后进行配置，而不是进行选择，因此我们的改进方法是在最优化求解时删除该条件，求解出最优权重后，对于负数的权重（代表卖空该基金）取等权比例的20%作为最低配置，剩余的基金按照最优权重的比例进行配置，这样可以保证每只基金均有配置。

改进结果如下：

对于改进后的模型，伯努利分布的Kelly公式的收益和夏普比率较未改进前基本持平，但是最大回撤幅度有所降低。正态分布下的Kelly公式收益和回撤下降幅度大于伯努利分布下的结果，这是因为之前正态分布权重偏离程度更大，总体正态分布下的Kelly公式收益在5.5%左右，最大回撤基本控制在6%左右，Calmar在2.8左右，夏普比率达到1.3，接近风险平价和波动率加权的夏普比率的水平。

从权重分布来看，权重间的差距（最大与最小权重的差）较改进之前显著降低，平均权重接近等权重水平，而伯努利分布的Kelly公式权重偏离程度高于正态分布下的，以基金数量为5的样本为例，伯努利分布的Kelly的最大权重为36.6%，正态分布的Kelly的最大权重为30%，同样在基金数量为10和20的样本也是如此。

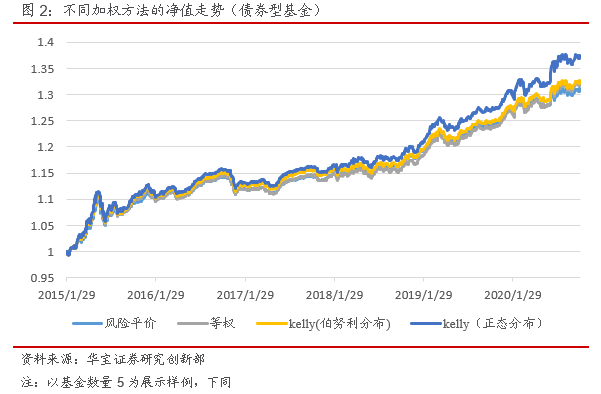
总体来看，Kelly公式的权重配置组合整体收益高于其他方法，但是风险也有所提升，其中，正态分布下的Kelly公式的权重配置组合收益最高，不过对于债券型基金来说收益差别不大，故风险控制在评价基金中更为重要，因此风险平价加权方法收益风险比更高。

2.2. 混合型基金组合测试结果

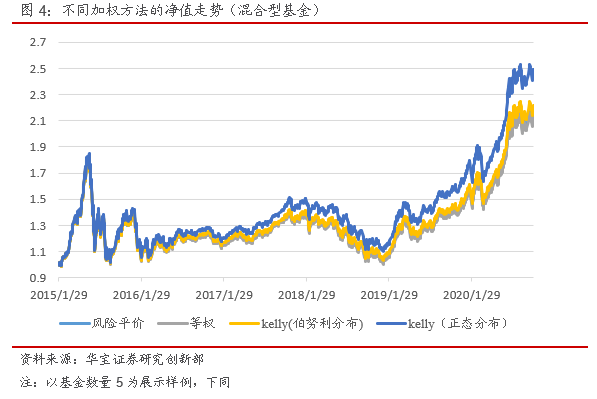
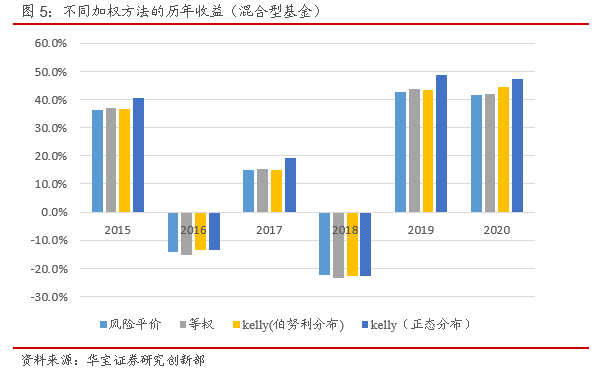
对于混合型基金，该类基金同时投资于股票、债券等资产，相对于债券型基金权益配置比例有所提高，收益和风险均有所增加，以等权重配置结果为例，年化收益在14%左右，最大回撤幅度达到45%，Calmar比例为0.9，夏普比率0.5左右。对比不同加权方法的结果，Kelly公式加权的组合收益高于其他两种方法，整体年化收益大于14%，其中正态分布下的Kelly收益最高，年化收益高于16%；从风险来看，风险平价回撤低于其他方法，年化波动率也是最低的，与债券型基金的测试结果一致，而伯努利分布下的Kelly公式、正态分布下的Kelly公式和等权配置差不多；总体从收益风险比来看，Kelly公式的整体收益风险比高于其他两种方法，Calmar比例大于1，夏普比率0.6左右，主要是因为对于混合型基金，Kelly公式加权方法下组合收益提升较为明显，同时风险没有明显增加，其中正态分布下的Kelly公式收益风险比最高。

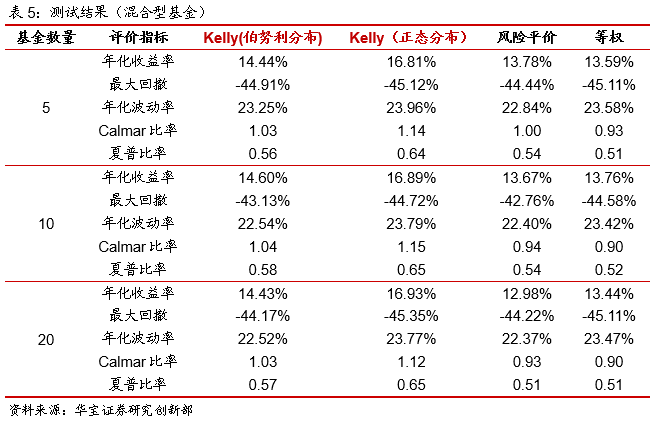
从权重分布来看，风险平价加权权重接近于等权重，而Kelly公式的变动幅度有所扩大，以基金数量为5的样本为例，风险平价最高配置比例为23%，最低权重为17.6%，Kelly公式最高权重高于30%，最低权重为4%，而伯努利分布的Kelly公式的权重偏离程度大于正态分布的Kelly公式，这与以债券型基金为样本的测试结果一致。

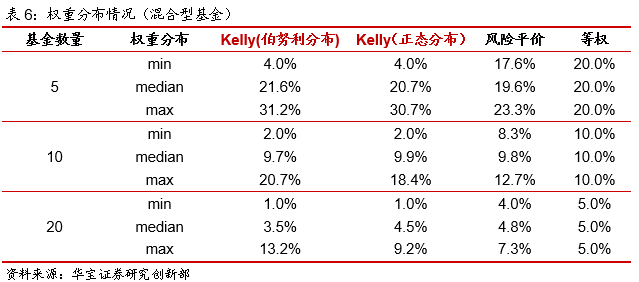
因此对于混合型基金，采用Kelly公式加权的组合收益高于风险平价和等权，风险水平与等权组合接近，但高于风险平价的加权方法，整体采用Kellly公式的加权的组合收益风险比较高，尤其是正态分布下的Kelly公式。

2.3. 股票型基金组合测试结果

对于股票型基金，是指股票持仓在80%以上的基金，以等权重配置结果为例，年化收益在9%左右，最大回撤达到44%左右，Calmar比例为0.6，夏普比率0.3左右。对比不同加权方法的结果，与混合型基金样本以及债券型基金样本的结果相同，Kelly公式的组合收益高于风险平价和等权，尤其是正态分布下的Kelly的收益最高，年化超过10%；从风险来看，Kelly公式加权的组合回撤整体低于风险平价和等权，正态分布下的Kelly公式的回撤较伯努利分布的Kelly公式的更小，在43%左右；从收益风险比来看，Kelly公式收益提升效果明显，但是回撤没有扩大，呈现Calmar比率和夏普比率高于风险平价和等权，其中正态分布下的Kelly公式收益风险比最高，Calmar比率在0.7附近，夏普比率达到0.4。

从权重分布来看，风险平价加权权重几乎接近于等权重，这表示股票型基金波动情况较为接近，但对于采用Kelly公式加权的组合，权重偏离幅度高于风险平价，对比不同基金数量的样本，伯努利分布的Kelly公式的权重偏离程度大于正态分布的Kelly公式，这与债券型基金的样本和股票型基金的样本测试结果一致。

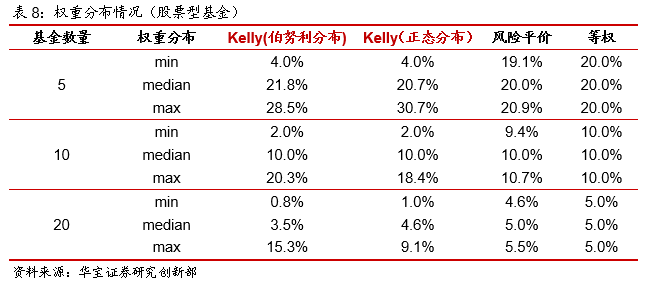
总体对于股票型基金，测试结果与混合型基金类似，Kelly公式加权的组合收益高于风险平价和等权，但是风险没有扩大，整体收益风险比有所提高，其中正态分布下的Kelly公式的加权方法收益风险比是最高的。

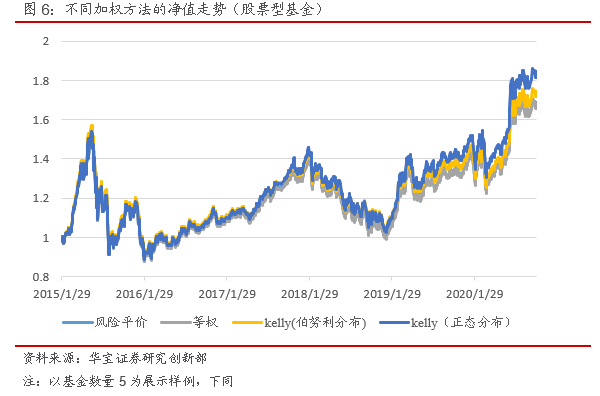
3. 结论

综上，本文尝试将Kelly公式应用在基金产品的权重配置上，为了保证测试的稳健性，我们以债券型基金、混合型基金以及股票型基金做为测试样本，并且考虑不同基金数量的影响。我们发现Kelly公式加权的组合收益高于风险平价和等权的组合，但是回撤和波动也有所扩大，而风险平价模型的风险控制较好。那么对于收益和风险较低的债券型基金，风险的控制对于收益风险比的提升更显著，因此风险平价模型收益风险比高于Kelly公式和等权加权的组合；对于收益和风险较高的混合型基金以及股票型基金，Kelly公式加权的组合收益明显提升同时回撤扩大不明显，总体收益风险比高于风险平价和等权加权的组合。对于Kelly公式，本文测试了资产价格为伯努利分布的Kelly公式和正态分布的Kelly公式，测试结果表明正态分布下的Kelly公式收益提升更明显，收益风险比也较高。